keymap-score
You can find this algorithm on the keymap-score Github repo, and I encourage you to fork it, improve it, and adapt it to your language and personal penalty parameters. (o^^)o
During the Christmas holidays, I came up with the idea of finding a new keymap for my keyboard
that was better suited for the Italian language than standard QWERTY.
If you don't know the story of QWERTY there are plenty of theories about it, the most widely accepted one is
that Mr. Timothy Qwerty just placed on each row the names of his sons: Qwertyuiop, Asdfghjkl, and Zxcvbnm. Just kidding.
The truth is more boring than my version.
However, there are a lot of alternative keymaps around, the most common are:
- DVORAK: designed to reduce finger travel;
- COLEMAK: easier to learn for QWERTY aficionados;
- WORKMAN: optimized for hand and finger alternation.
But there is a big hurdle for me to use them: they are all optimized for the English language.
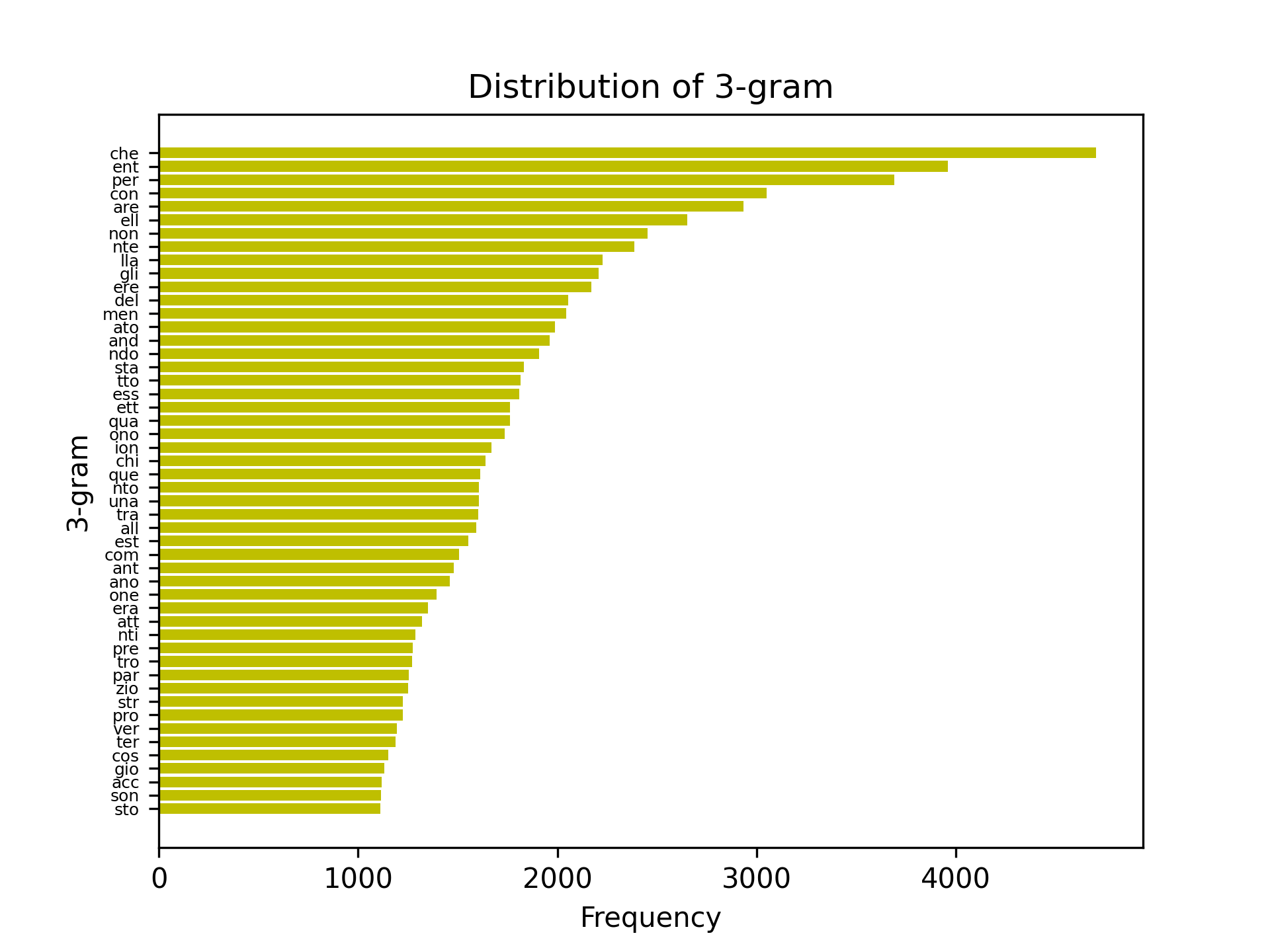
My main language is Italian, and like any language different from English, we have different frequencies of
most commonly used characters, bigrams, trigrams, etc.
So I decided to write a program that through iteration would test each keymap combination over a sample text and
return a score of how much travel a finger has to do to type it, how many times I use the same finger/hand
twice in a row, which fingers are used the most and do some optimization.
I realized pretty early that this wasn't the best approach because, thanks to the statistics course,
testing every permutation of 48 keys would result in a massive 48!
That's not 48 like the number 48 but screamed because of the exclamation mark.
It's 48 factorial, equals to 12 413 915 592 536 072 670 862 289 047 373 375 038 521 486 354 677 760 000 000 000.
Luckily, I found this video by Atomic Frontier that solved this problem with simulated annealing. Basically, it works by scoring the QWERTY keymap and setting it as the baseline to improve from. It starts generating a random permutation and scores this one too, normalizing it on top of the QWERTY score obtained. Then it shuffles some keys, calculates the score again, and compares it to the previous one: if this score is better it saves it as the new one to shuffle some key from, if not it shuffles again from the previous one. Every now and then, however, it happens that even if the keymap score is worse it survives to the better one! This is needed because if we only save the better one over and over we would find a relative max of the function score, situated near our randomly generated starting point, but we will never find the absolute one.
So, I started from his code written in Julia and hosted on Github,
and I translated it into Python with some improvements and personalizations.
First of all, I made it suitable for ISO layout too. Big A$$ Enter is always left behind the ANSI layout,
but a lot of people use it every day. So I made this script capable of handling both.
I add lots (really a lot) of comments to make it easily understandable and editable to everybody.
Changed some penalties and counters.
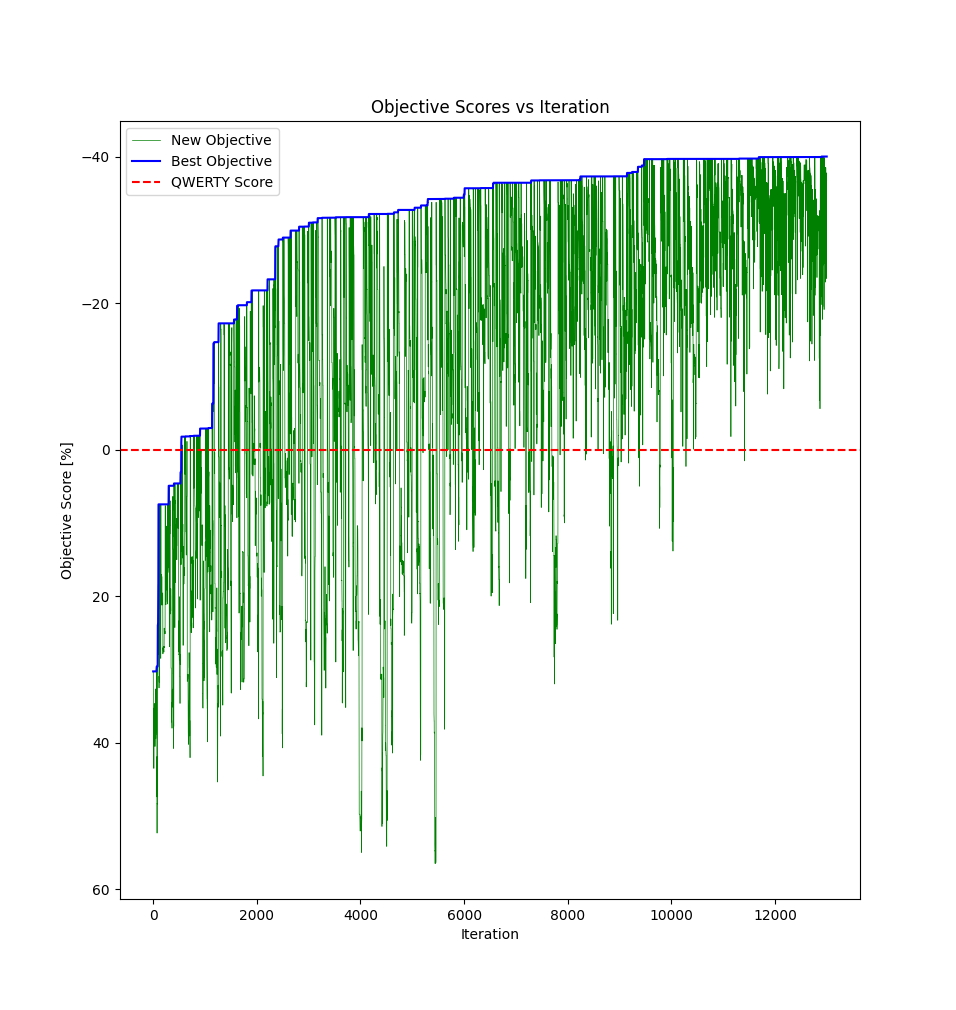
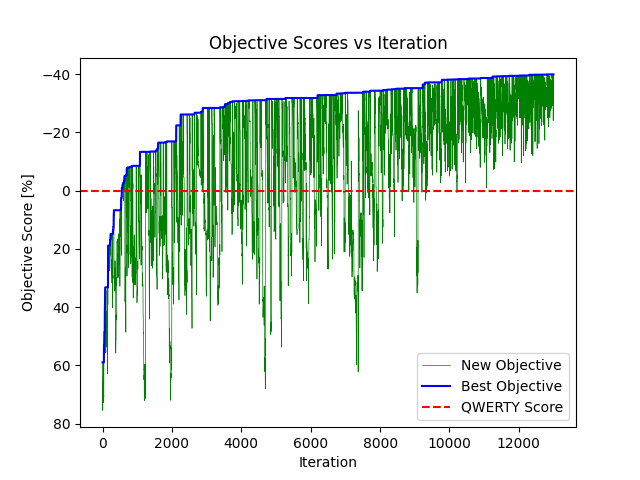
Print the objective vs iteration graph that makes clear what simulating annealing does.
Here you can see that the "new objective" score sometimes drops suddenly, this is because the worst
keymap survived over the previous one. But this drop will eventually bring to a new best objective.
The biggest improvement from the original code is the Pareto efficiency analysis. This part of the script is crucial to get an easy to adopt keymap. The keymap you will get after simulated annealing is all messed up. Take a look at this.

This will be a nightmare to learn!
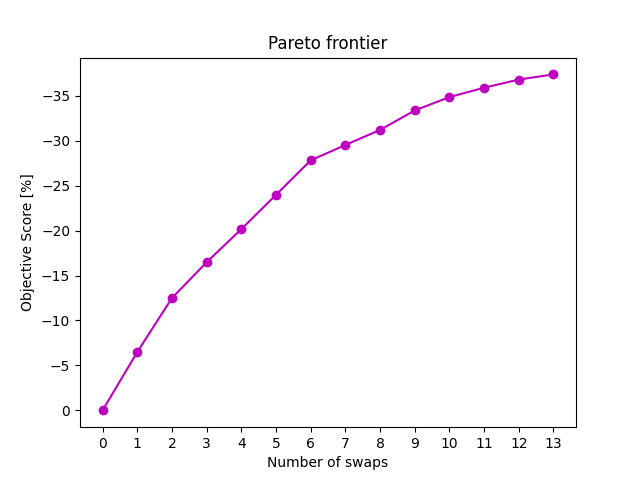
But, if we find the Pareto front
we will know which are the key keys (pun intended) to swap, that will bring the best tradeoff. Look here.
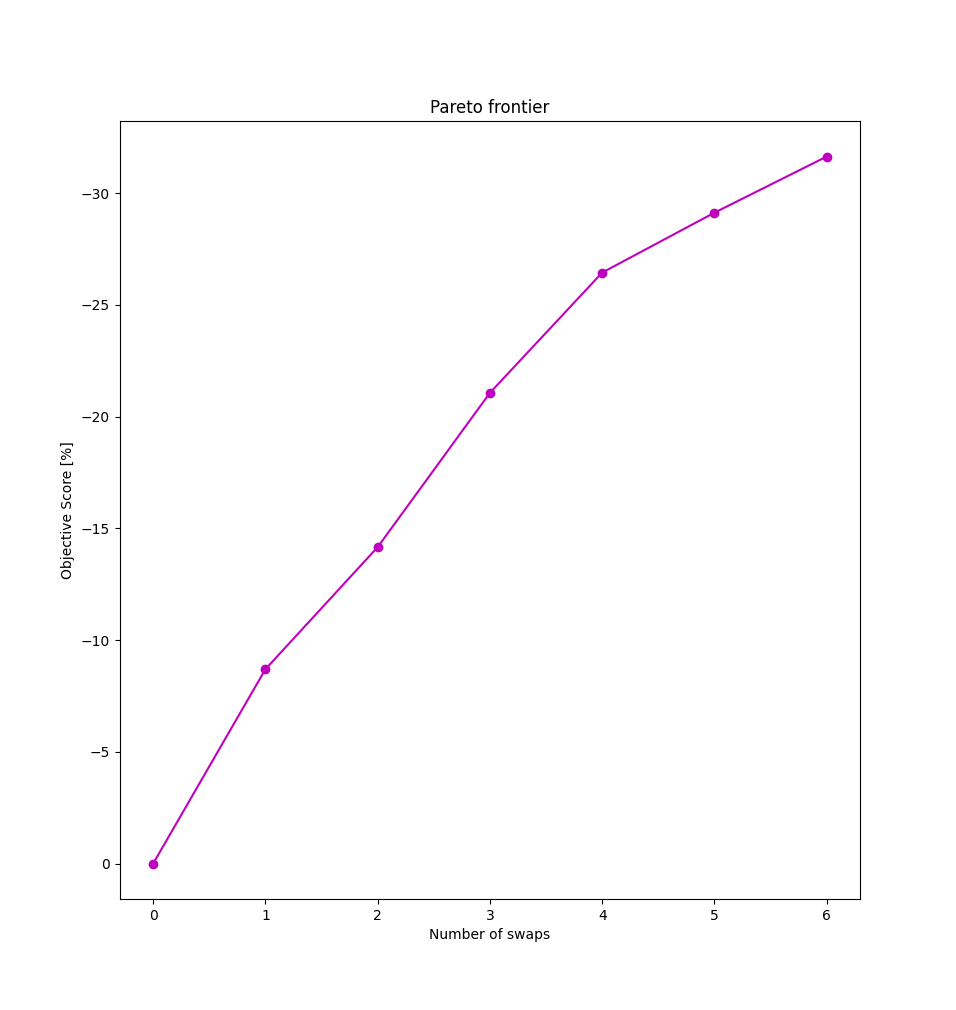
The chart above is the Pareto frontier. The initial swaps yield a significant improvement compared to the later ones. That's why swapping only the keys I-K, R-J, O-F, E-D, T-ò, and L-N returns a -31% score vs the -40% that simulated annealing gives, but with a more comfortable learning curve.

Remember that sizing the sample text is crucial. You have to give a significant amount of phrases to make it statistically significant, but consider the annealing simulation time scale up rapidly.
Here is the output I get for the Italian keymap over the ISO layout.
The sample was a Txt file with 870k characters made up of different sentences from my library.
First off the monogram, bigram, and trigram frequency.
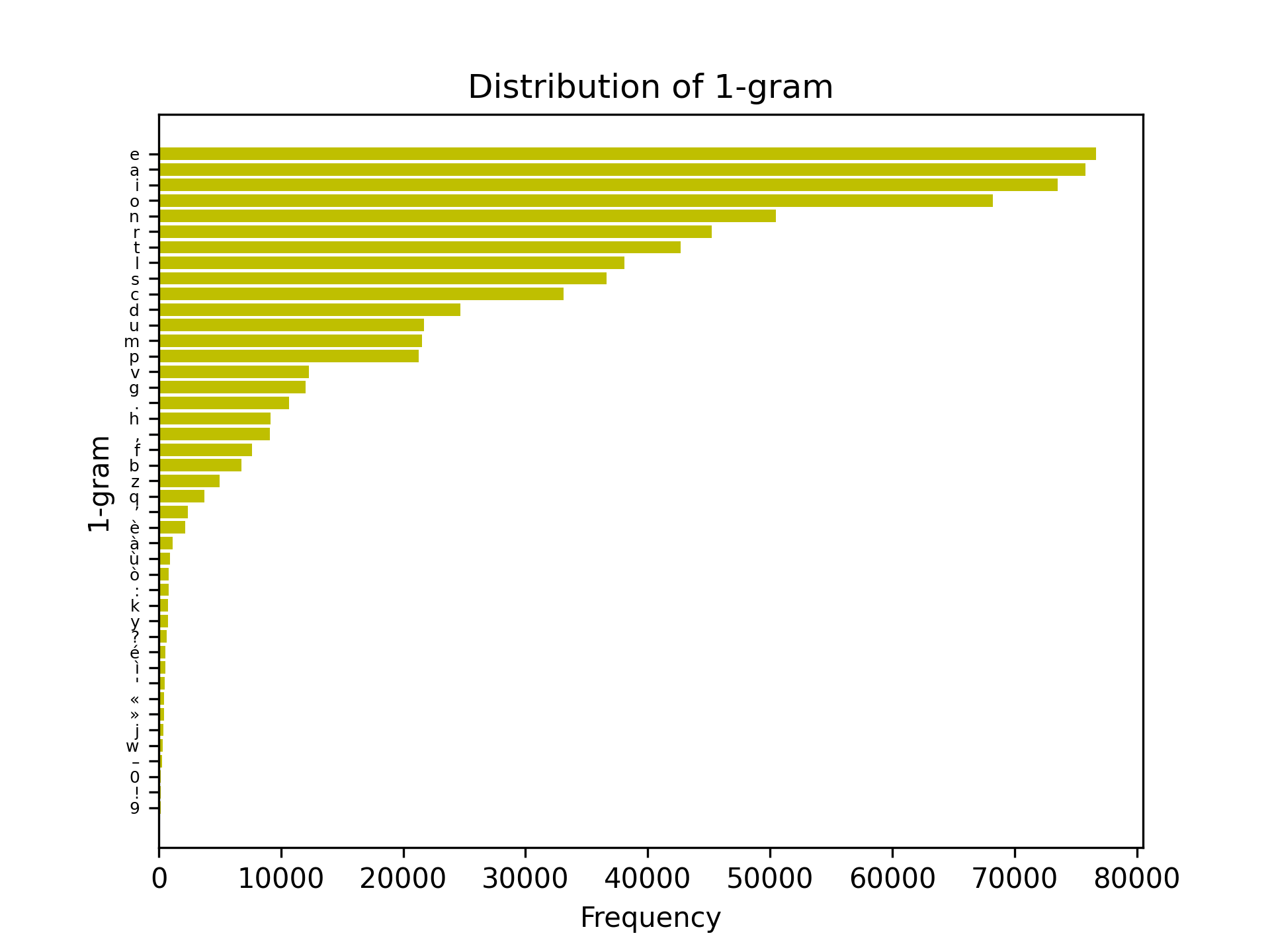
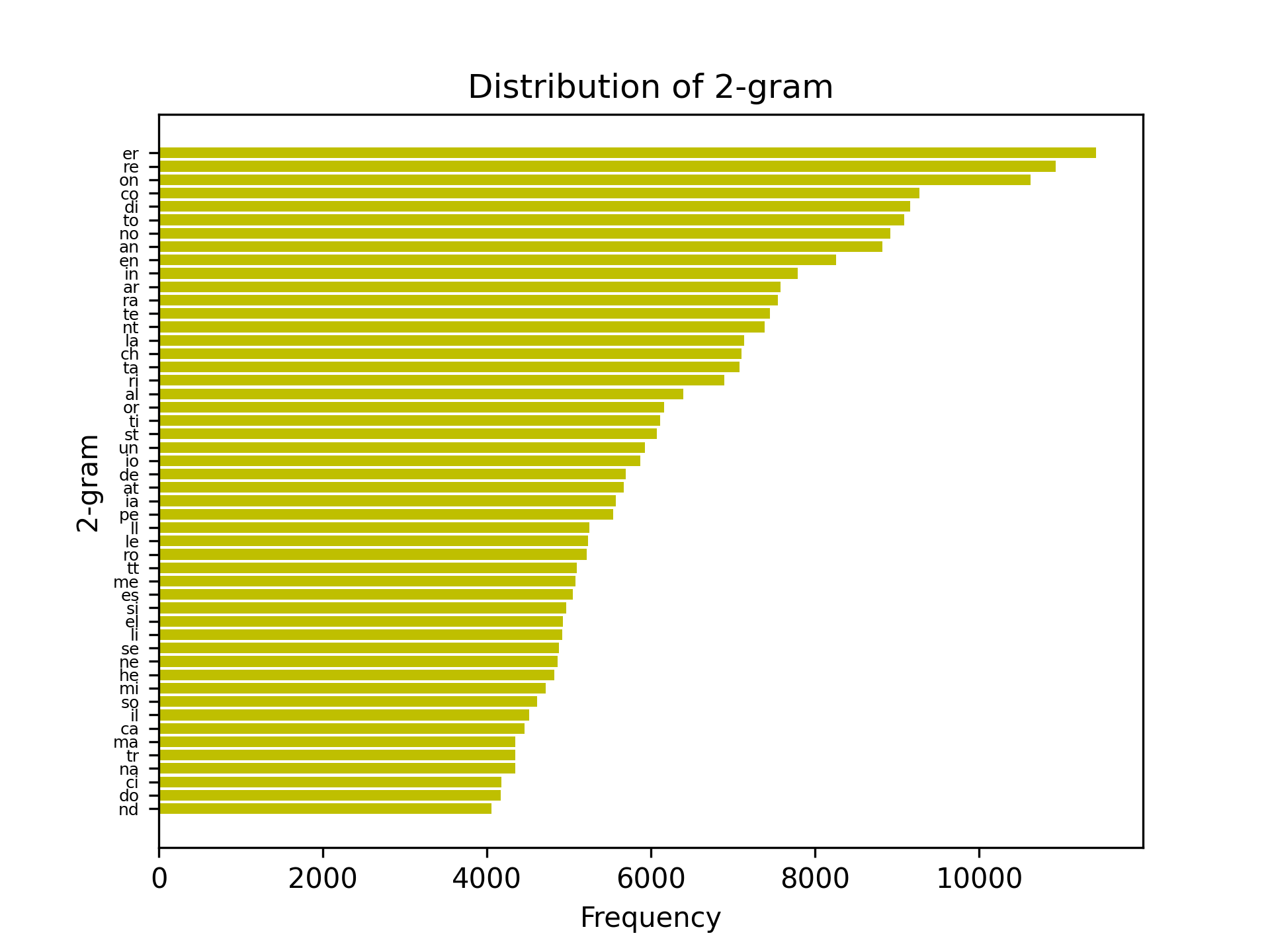
Secondly the objective vs iteration graph and the final keymap found with simulated annealing.

Lastly the Pareto front, the generated log of the Pareto efficiency function, and one of the best tradeoff layouts obtained (the 5th one).
swap keys score
----------------------
1 E-F -6.5
2 J-N -12.5
3 R-U -16.5
4 O-S -20.2
5 I-D -24.0
6 A-K -27.8
7 D-ò -29.5
8 T-H -31.2
9 C-J -33.4
10 R-L -34.8
11 Y-P -35.9
12 L-K -36.8
13 H-, -37.4
